library(tidyverse)
library(readxl)
###Importar os dados
dados=read_excel("notas.xlsx",1)4 Aplicações Básicas e Intermediárias em IA com R
Este capítulo apresenta uma visão abrangente das aplicações práticas da Inteligência Artificial (IA) utilizando o R. Cobrindo desde técnicas básicas até métodos intermediários, ele oferece aos leitores uma base sólida em teoria e prática. Os tópicos incluem Regressão Linear e Logística, Árvores de Decisão e Florestas Aleatórias, além de uma introdução a Redes Neurais. O capítulo também discute as tendências e avanços recentes em Machine Learning, proporcionando aos leitores insights sobre as futuras inovações no campo da IA.
4.1 Regressão Linear
A regressão linear é um método fundamental tanto em estatística quanto em machine learning. Ela é utilizada para modelar a relação entre uma variável de saída (dependente) contínua e uma ou mais variáveis de entrada (independentes). Esse método estabelece uma equação linear que descreve a relação entre essas variáveis, permitindo a previsão de valores da variável de saída com base em novos dados de entrada. Apesar de sua simplicidade, a regressão linear é uma ferramenta poderosa para análises preditivas e é frequentemente o ponto de partida para muitos estudos e análises em diversos campos (Zbicki and Santos 2020; James et al. 2023; Burger 2018).
Conceito: A ideia central da regressão linear é encontrar a melhor reta (ou, em casos de múltiplas variáveis independentes, um plano ou hiperplano) que se ajuste aos dados observados.
A reta (plano ou hiperplano) é obtida minimizando a diferença entre os valores reais observados nos dados e os valores previstos pelo modelo. Essa minimização geralmente é realizada através do método dos mínimos quadrados, buscando reduzir a soma dos quadrados das diferenças entre os valores observados e os previstos. Esse método fornece uma maneira eficiente de estimar os coeficientes do modelo linear, oferecendo uma previsão confiável baseada nas variáveis independentes (Singh and Allen 2016; Zbicki and Santos 2020).
A regressão linear é valiosa tanto para visualizar tendências quanto para fazer previsões. Ao ajustar uma linha a um conjunto de pontos de dados, ela facilita a visualização e a compreensão da relação entre as variáveis. Esta técnica se torna especialmente útil em grandes conjuntos de dados, onde pode ser desafiador identificar padrões. Por meio da regressão linear, torna-se mais simples discernir a relação entre variáveis, proporcionando informações que podem guiar análises mais profundas e decisões baseadas em dados (Singh and Allen 2016; Zbicki and Santos 2020):
Interpretação Gráfica: A linha de regressão em um gráfico oferece uma interpretação visual imediata da relação entre as variáveis. Por exemplo, uma linha de regressão ascendente indica uma relação positiva, significando que à medida que uma variável aumenta, a outra também tende a aumentar.
Identificação de Anomalias: Além de revelar tendências, a regressão linear ajuda a identificar outliers ou anomalias nos dados, que são pontos significativamente afastados da linha de regressão.
As aplicações práticas da regressão linear são vastas, abrangendo áreas como economia, meteorologia, saúde e mais, fornecendo previsões valiosas e insights para tomadas de decisão (Singh and Allen 2016; Zbicki and Santos 2020).
Previsões Baseadas em Dados: Ao ajustar um modelo de regressão linear, é obtido uma equação que pode ser usada para fazer previsões. Por exemplo, em um modelo de regressão linear simples, essa equação pode ter a forma \(y=mx+b\), em quende \(y\) é a variável de sáida (dependente), \(x\) é a variável de entrada (independente), \(m\) é a inclinação e \(b\) é o intercepto da linha de regressão.
Aplicações Práticas: As previsões têm inúmeras aplicações práticas em diversos campos, como economia (previsão de tendências de mercado), meteorologia (previsão de temperaturas futuras), saúde (previsão de taxas de recuperação de pacientes), entre muitos outros.
Ao trabalhar com regressão linear, é crucial considerar alguns aspectos importantes (Singh and Allen 2016; Chan 2015):
Qualidade dos Dados: A eficácia da regressão linear está diretamente relacionada à qualidade dos dados utilizados. Dados imprecisos, incompletos ou com erros podem resultar em previsões falhas ou enganosas.
Relações Lineares: A regressão linear é ideal para situações em que a relação entre as variáveis é de fato linear. Se a relação for não-linear, modelos de regressão linear podem não ser adequados. Nestes casos podem ser aplicados modelos de regressão não linear e outras técnicas de machine learning podem ser mais apropriadas.
Relações Lineares: A regressão linear é ideal para situações onde há uma relação linear entre as variáveis .Em cenários onde essa relação é não-linear a aplicação de modelos de regressão não linear ou outras técnicas de machine learning pode ser mais apropriada, permitindo uma modelagem mais precisa das complexidades inerentes aos dados.
Causalidade vs. Correlação: É importante lembrar que a regressão linear por si só não implica causalidade. Ela pode identificar correlações entre variáveis, mas isso não implica uma relação de causa e efeito direta.
4.1.1 Exemplo Prático
Vamos considerar um conjunto de dados hipotético que representa o desempenho de alunos em uma determinada disciplina. O objetivo é analisar a relação entre vários fatores relacionados aos hábitos de estudo e o desempenho final dos alunos (medido em notas). Espera-se que essa relação seja aproximadamente linear, com a nota final variando de acordo com diferentes variáveis como o número de horas de estudo, frequência nas aulas e outros fatores comportamentais e socioeconômicos. Vamos utilizar o banco de dados Notas.xlsx
Para ilustrar, vamos gerar dados de notas de alunos com base nos seguintes fatores:
- \(X_1\): O número de horas de estudo por semana.
- \(X_2\): O número de faltas durante o semestre.
- \(X_3\): A nota média em avaliações intermediárias.
- \(X_4\): O nível de escolaridade dos pais (1: Ensino Fundamental, 2: Ensino Médio, 3: Ensino Superior).
- \(X_5\): O uso de recursos de aprendizagem online (horas por semana).
Vamos ajustar um modelo de regressão linear e visualizá-lo com pacote ggplot2(Wickham 2016) :
#Ajustar um modelo de regressão linear e visualizá-lo com pacote ggplot2
modelo <- lm(Y ~ X1 , data = dados)
summary(modelo)
Call:
lm(formula = Y ~ X1, data = dados)
Residuals:
Min 1Q Median 3Q Max
-20.120 -6.187 -1.350 5.992 36.602
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 90.5494 4.2581 21.265 < 2e-16 ***
X1 2.5125 0.5324 4.719 7.88e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 9.594 on 98 degrees of freedom
Multiple R-squared: 0.1852, Adjusted R-squared: 0.1769
F-statistic: 22.27 on 1 and 98 DF, p-value: 7.879e-06ggplot(dados, aes(x = X1, y = Y)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE) +
theme_minimal() 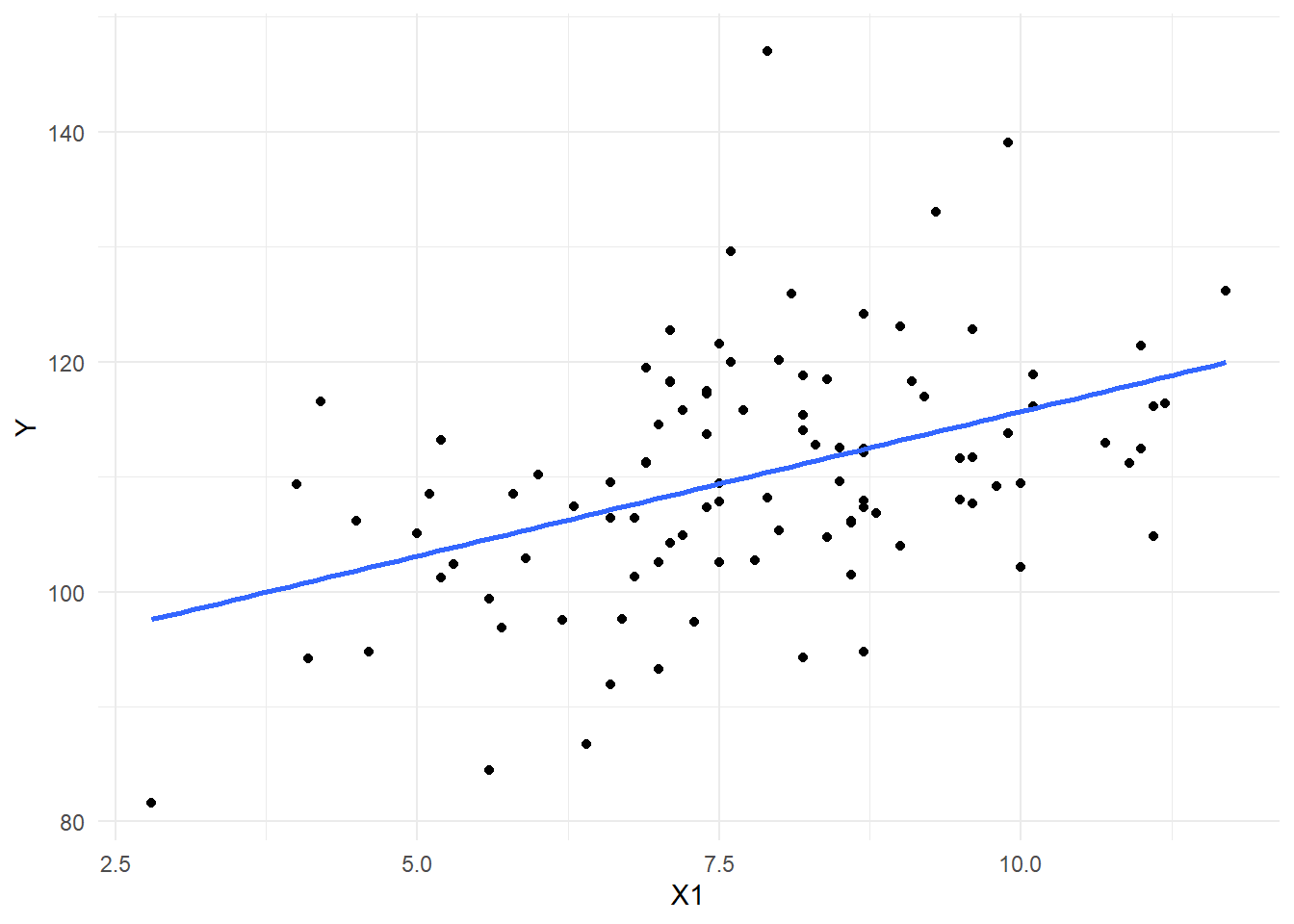
Neste exemplo, o modelo de regressão é representado pela equação \(y=90,5494+2,5125X\) e ilustrado pela linha no gráfico, destacando a relação entre temperatura e consumo de energia. Os pontos no gráfico representam os dados observados, enquanto a linha demonstra a tendência geral. Isso sugere que existe uma correlação positiva entre o aumento da temperatura e o aumento no consumo de energia, com a linha de regressão oferecendo uma visualização clara dessa tendência.
Utilizando o mesmo exemplo da relação entre as horas de estudo e o desempenho final dos alunos, agora vamos explorar como o modelo de regressão linear pode ser usado para fazer previsões. O objetivo é estimar a nota final com base no número de horas de estudo.
Com o modelo ajustado, podemos usar a função predict() para fazer previsões. Por exemplo, se quisermos prever a nota final para 6, 8, 10, e 12 horas de estudo por semana, fazemos o seguinte:
horas_novas <- data.frame(X1 = c(6, 8, 10, 12))
previsao_notas <- predict(modelo, newdata = horas_novas)
previsao_notas 1 2 3 4
105.6246 110.6496 115.6747 120.6997 4.2 Regressão linear multipla
A Regressão Linear Múltipla é uma técnica estatística usada para modelar a relação entre uma variável dependente (ou variável resposta) e duas ou mais variáveis independentes (ou variáveis explicativas). Enquanto na regressão linear simples há apenas uma variável independente, na regressão múltipla consideramos várias variáveis ao mesmo tempo, permitindo uma análise mais completa de cenários onde múltiplos fatores influenciam o resultado.
4.2.1 Objetivo da Regressão Múltipla
O objetivo da regressão linear múltipla é estimar como cada variável independente contribui para a variação na variável dependente e fazer previsões. A equação da regressão múltipla é representada da seguinte forma:
[ Y = _0 + _1 X_1 + _2 X_2 + + _n X_n + ]
Onde: - ( Y ) é a variável dependente (o que queremos prever ou explicar). - ( _0 ) é o intercepto, ou seja, o valor de ( Y ) quando todas as variáveis independentes são iguais a zero. - ( _1, _2, , _n ) são os coeficientes de regressão que indicam o impacto de cada variável ( X_1, X_2, , X_n ) na variável dependente ( Y ). - ( ) é o termo de erro, representando a variação em ( Y ) que não pode ser explicada pelos ( X )’s.
4.2.2 Exemplo Prático: Previsão de Notas
No contexto de dados educacionais, a regressão múltipla pode ser usada para prever a nota final de um aluno com base em múltiplos fatores, como: - ( X_1 ): Horas de estudo por semana. - ( X_2 ): Número de faltas. - ( X_3 ): Nota nas avaliações intermediárias. - ( X_4 ): Nível de escolaridade dos pais. - ( X_5 ): Uso de recursos online.
Cada uma dessas variáveis pode ter um efeito diferente sobre a nota final, e a regressão múltipla nos permite quantificar esses efeitos e prever o desempenho dos alunos.
Interpretação dos Coeficientes
- **( _1 )**: Representa o quanto a nota final muda, em média, para cada hora adicional de estudo.
- **( _2 )**: Indica o impacto que uma falta a mais tem na nota final.
- **( _3 )**: Reflete a contribuição das notas intermediárias na previsão da nota final.
- **( _4 )**: Avalia o efeito do nível de escolaridade dos pais no desempenho do aluno.
- **( _5 )**: Mostra como o uso de recursos online afeta o desempenho acadêmico.
# Ajustando o modelo de regressão linear múltipla
modelo_completo <- lm(Y ~ X1 + X2 + X3 + X4 + X5, data =dados)
# Resumo do modelo
summary(modelo_completo)
Call:
lm(formula = Y ~ X1 + X2 + X3 + X4 + X5, data = dados)
Residuals:
Min 1Q Median 3Q Max
-12.1986 -3.2309 -0.0773 3.5939 12.4919
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 43.35695 5.14124 8.433 3.91e-13 ***
X1 2.62655 0.30458 8.623 1.55e-13 ***
X2 -1.48825 0.18768 -7.930 4.49e-12 ***
X3 0.53121 0.05366 9.899 3.01e-16 ***
X4 1.92567 0.69683 2.763 0.00688 **
X5 1.97781 0.41280 4.791 6.18e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5.407 on 94 degrees of freedom
Multiple R-squared: 0.7517, Adjusted R-squared: 0.7385
F-statistic: 56.92 on 5 and 94 DF, p-value: < 2.2e-16Com base nos coeficientes fornecidos, a equação de regressão múltipla pode ser escrita da seguinte forma:
[ Y = 43.36 + 2.63X_1 - 1.49X_2 + 0.53X_3 + 1.93X_4 + 1.98X_5 ]
O valor de ( R^2 ) indica a proporção da variação na variável dependente ( Y ) que pode ser explicada pelo modelo de regressão. Se o ( R^2 ) for, por exemplo, 0.85, isso significa que 85% da variação nas notas finais dos alunos pode ser explicada pelas variáveis independentes ( X_1 ), ( X_2 ), ( X_3 ), ( X_4 ), e ( X_5 ). Quanto mais próximo de 1, maior o poder explicativo do modelo.
4.2.3 Interpretação dos Coeficientes
Intercepto (43.36): Quando todas as variáveis independentes são iguais a zero, a nota final prevista será 43.36.
( X_1 ) (Horas de estudo por semana, coeficiente: 2.63): Para cada hora adicional de estudo por semana, espera-se que a nota final aumente, em média, em 2.63 pontos, mantendo todas as outras variáveis constantes. O valor ( p )-value ( (< 2 ^{-13}) ) indica que o coeficiente é altamente significativo.
( X_2 ) (Número de faltas, coeficiente: -1.49): Para cada falta a mais, a nota final é reduzida em 1.49 pontos, em média, com as outras variáveis mantidas constantes. O coeficiente negativo e o ( p )-value ( (< 4.49 ^{-12}) ) indicam que faltas afetam negativamente o desempenho dos alunos de maneira significativa.
( X_3 ) (Nota nas avaliações intermediárias, coeficiente: 0.53): A cada ponto adicional nas notas intermediárias, a nota final aumenta em 0.53 pontos, em média. Isso significa que o desempenho nas avaliações anteriores tem um impacto positivo no resultado final, sendo este coeficiente também altamente significativo ( (p < 3.01 ^{-16}) ).
( X_4 ) (Escolaridade dos pais, coeficiente: 1.93): Se o nível de escolaridade dos pais aumenta (por exemplo, de Ensino Médio para Ensino Superior), espera-se que a nota final dos alunos aumente em 1.93 pontos, em média. O ( p )-value ( (0.00688) ) sugere que essa variável também é significativa, mas com um impacto menos expressivo em comparação a outras variáveis.
( X_5 ) (Uso de recursos online, coeficiente: 1.98): Para cada hora adicional de uso de recursos online, a nota final aumenta em 1.98 pontos, em média. Isso mostra que o uso de ferramentas de aprendizado online está positivamente associado ao desempenho dos alunos, com alta significância ( (p < 6.18 ^{-6}) ).
4.3 Regressão Logística
A regressão logística é uma técnica estatística usada para modelar a probabilidade de ocorrência de um evento, categorizando o resultado em classes. Esta técnica é empregada para variáveis dependentes categóricas binárias, como “sim” ou “não”, e “sucesso” ou “fracasso”. Ela difere da regressão linear, que prevê valores contínuos, ao estimar a probabilidade de um evento ocorrer, baseando-se em um ou mais preditores. A regressão logística é particularmente útil em classificadores de aprendizado de máquina, sendo um componente chave dos modelos lineares generalizados(Zbicki and Santos 2020; James et al. 2023; Burger 2018).
A regressão logística, utilizada no contexto de classificadores, pode ser expressa matematicamente para uma classe binária da seguinte maneira:
\[ Y_i = 1 \Rightarrow P( Y_i=1)=\pi_i\\ Y_i = 0 \Rightarrow P( Y_i=0)=1-\pi_i\\ \]
O modelo de regressão logistica é dado por: \[ \pi(X)=\frac{e^{\beta_0+\beta_1X_1+\beta_2X_2+...+\beta_mX_m}}{1+e^{\beta_0+\beta_1X_1+\beta_2X_2+...+\beta_mX_m}} \]
em que \(X\) representa o conjunto de atributos ou variáveis de entrada.
Ao trabalhar com regressão logística, é crucial considerar aspectos importantes como:
Relação entre Variáveis: Este método é eficaz quando há uma relação clara entre as variáveis independentes e a variável dependente binária. As variáveis independentes podem ser categóricas ou quantitativas, mas para variáveis quantitativas, é importante verificar se existe uma relação log-log.
Multicolinearidade: É essencial evitar alta correlação entre as variáveis independentes, pois isso pode comprometer a interpretação dos coeficientes do modelo.
Avaliação do Modelo: Para avaliar a precisão e eficácia do modelo, deve-se usar métricas apropriadas, como a área sob a curva ROC (AUC).
Exemplo Prático
Implementação no R
No R, a função glm() com a família binomial é comumente usada para realizar regressão logística.
Para ilustrar a utilização da regressão logística, vamos utilizar um conjunto de dados hipotético contendo informações sobre o desempenho acadêmico de alunos. Este conjunto de dados foi gerado com base em 73 observações e contém 6 variáveis que podem influenciar se um aluno foi aprovado ou reprovado em uma disciplina.
As variáveis presentes no conjunto de dados são as seguintes:
Horas de estudo por semana (X1): Número de horas que o aluno dedica aos estudos semanalmente.
Número de faltas (X2): Quantidade de faltas acumuladas pelo aluno ao longo do semestre.
Nota nas avaliações intermediárias (X3): Média das notas obtidas nas avaliações realizadas antes do exame final.
Nível de escolaridade dos pais (X4): Representa o nível de escolaridade dos pais, sendo 1 para Ensino Fundamental, 2 para Ensino Médio, e 3 para Ensino Superior.
Uso de recursos online (X5): Número de horas semanais que o aluno utiliza recursos de aprendizado online.
Aprovado (Y): Resultado binário, onde 1 indica que o aluno foi aprovado e 0 indica que foi reprovado.
Esse conjunto de dados é ideal para aplicar a regressão logística, pois a variável dependente é categórica (aprovado/reprovado). O objetivo é prever a probabilidade de um aluno ser aprovado com base nos fatores mencionados. O banco de dados utilizado é aprovacao.xlsx
library(tidyverse)
library(readxl)
###Importar os dados
dados=read_excel("aprovacao.xlsx",1)
Call:
glm(formula = Y ~ X1 + X2 + X3 + X4 + X5, family = binomial,
data = dados)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -6.21944 3.28756 -1.892 0.05852 .
X1 0.54735 0.20532 2.666 0.00768 **
X2 -0.23566 0.10803 -2.181 0.02915 *
X3 0.04278 0.03465 1.235 0.21690
X4 -0.19819 0.40855 -0.485 0.62759
X5 0.30652 0.19890 1.541 0.12329
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 87.608 on 72 degrees of freedom
Residual deviance: 72.842 on 67 degrees of freedom
AIC: 84.842
Number of Fisher Scoring iterations: 5Análise dos Coeficientes com Base nos Valores-p e Interpretação das Odds:
1. Intercepto (p = 0.05852):
- O valor-p está próximo de 0.05, indicando que o intercepto é marginalmente significativo. Isso sugere que, na ausência das variáveis explicativas (( X_1 ), ( X_2 ), ( X_3 ), ( X_4 ), ( X_5 )), a probabilidade de aprovação ou reprovação não é fortemente diferente de zero.
- Como está próximo, não podemos afirmar com total confiança que ele impacta diretamente a probabilidade de aprovação.
2. ( X_1 ) - Horas de Estudo por Semana (p = 0.00768):
- O valor-p é menor que 0.01, indicando que essa variável é altamente significativa. Isso significa que o número de horas de estudo por semana tem um impacto estatisticamente significativo na probabilidade de aprovação dos alunos.
- Interpretação das Odds: Se o coeficiente de ( X_1 ) for, por exemplo, \(\beta_1 = 0.5\), então \(\exp(0.5)=1.65\). Isso indica que, para cada hora adicional de estudo por semana, as odds de aprovação aumentam em cerca de 65%. Em outras palavras, mais horas de estudo aumentam a probabilidade de aprovação de maneira significativa.
3. ( X_2 ) - Número de Faltas (p = 0.02915):
- O valor-p é menor que 0.05, o que indica que essa variável também é significativa. Isso sugere que o número de faltas influencia significativamente a probabilidade de aprovação dos alunos.
- Interpretação das Odds: Supondo que o coeficiente de ( X_2 ) seja \(\beta_2=-0.3\), então \(\exp(-0.3)=0.74\). Isso indica que, para cada falta adicional, as odds de aprovação diminuem em cerca de 26%. Ou seja, mais faltas reduzem significativamente a probabilidade de aprovação.
4. ( X_3 ) - Nota nas Avaliações Intermediárias (p = 0.21690):
- O valor-p é maior que 0.05, indicando que essa variável não é significativa. Isso significa que as notas intermediárias não têm uma influência significativa na probabilidade de aprovação, quando controladas pelas outras variáveis.
5. ( X_4 ) - Escolaridade dos Pais (p = 0.62759):
- O valor-p é bem maior que 0.05, sugerindo que o nível de escolaridade dos pais não é um fator significativo para a probabilidade de aprovação dos alunos.
6. ( X_5 ) - Uso de Recursos Online (p = 0.12329):
- O valor-p é maior que 0.05, indicando que o uso de recursos online não tem um efeito significativo na probabilidade de aprovação.
As odds fornecem uma interpretação clara de como as variáveis significativas afetam a probabilidade de aprovação, mostrando que o aumento nas horas de estudo favorece a aprovação, enquanto o aumento no número de faltas prejudica as chances de sucesso dos alunos.
4.3.1 Seleção de Variáveis
require(SignifReg)Carregando pacotes exigidos: SignifRegWarning: package 'SignifReg' was built under R version 4.3.3modelo1 = SignifReg(modelo,alpha = 0.05,direction = "both",criterion = "p-value",adjust.method = "fdr")Warning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomial
Warning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomial
Warning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialWarning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomial
Warning in drop1.glm(fit2, test = "F"): O teste F assume a família
quasibinomialWarning in drop1.glm(fit, test = "F"): O teste F assume a família quasibinomialsummary(modelo1)
Call:
glm(formula = Y ~ X1, family = binomial, data = dados)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.0489 1.2287 -1.667 0.0954 .
X1 0.3919 0.1638 2.393 0.0167 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 87.608 on 72 degrees of freedom
Residual deviance: 81.130 on 71 degrees of freedom
AIC: 85.13
Number of Fisher Scoring iterations: 4O modelo de regressão logística ajustado mostra que a variável ( X_1 ) foi selecionada como significativa no modelo. Vamos interpretar os resultados apresentados no summary do modelo, com foco no valor-p, odds, e a possível interação entre a seleção de variáveis e sua significância.
1. Coeficiente do Intercepto:
- Estimativa: (-2.0489)
- Erro padrão: (1.2287)
- Valor-p: (0.0954)
O intercepto não é altamente significativo (valor-p ( ), ligeiramente maior que 0.05). Isso indica que, na ausência de ( X_1 ), a probabilidade de ocorrência do evento de interesse não é fortemente diferente de zero, mas há uma tendência marginal para rejeitar a hipótese nula.
2. Coeficiente de ( X_1 ) - Horas de Estudo por Semana:
- Estimativa: (0.3919)
- Erro padrão: (0.1638)
- Valor-p: (0.0167)
O valor-p associado ao coeficiente de ( X_1 ) é (0.0167), o que indica que ( X_1 ) é estatisticamente significativa ao nível de significância de 5% (( = 0.05 )). Isso significa que o número de horas de estudo por semana afeta significativamente a probabilidade de aprovação.
Interpretação das Odds:
O coeficiente de ( X_1 ) \(\beta_1=0.3919\) pode ser interpretado em termos de odds: - As odds de aprovação associadas a
\(X_1\) são \(\exp(0.3919) \approx 1.48\). Isso significa que, para cada hora adicional de estudo por semana, as odds de aprovação aumentam em cerca de 48%.
Relação entre as Variáveis e o Processo de Seleção:
O processo de seleção de variáveis, especialmente quando usamos métodos como o SignifReg com critérios baseados no valor-p e o método de ajuste de múltiplos testes (como o FDR - False Discovery Rate), pode resultar na retirada de variáveis que não são significativamente importantes para o modelo. Esse ajuste é essencial para reduzir o risco de sobreajuste (overfitting) e garantir que o modelo seja parcimonioso.
No caso do seu modelo, apenas ( X_1 ) foi mantida como significativa. É importante observar que a significância de uma variável pode ser afetada pela inclusão ou exclusão de outras variáveis. Por exemplo:
Colinearidade: Quando duas ou mais variáveis explicativas estão fortemente correlacionadas, pode ser difícil determinar a significância de uma variável isolada. A inclusão de uma variável correlacionada pode mascarar a verdadeira relação de outra variável com a variável resposta.
Impacto da Exclusão de Variáveis: Se uma variável insignificante for removida, isso pode aumentar ou reduzir a significância de outras variáveis no modelo. O método de seleção baseado em valor-p ajustado com o FDR tem como objetivo minimizar esses problemas, garantindo que apenas as variáveis mais robustas sejam mantidas.
Carregando pacotes exigidos: caretCarregando pacotes exigidos: lattice
Attaching package: 'caret'The following object is masked from 'package:purrr':
lifty1_prob <- predict(modelo1, type = "response") # Previsão como probabilidades
# Converter probabilidades em valores binários (0 ou 1) com um limiar de 0.5
y1 <- ifelse(y1_prob > 0.5, 1, 0)
# Matriz de confusão
conf_matrix <- confusionMatrix(as.factor(y1), as.factor(dados$Y))
conf_matrixConfusion Matrix and Statistics
Reference
Prediction 0 1
0 3 4
1 18 48
Accuracy : 0.6986
95% CI : (0.58, 0.8006)
No Information Rate : 0.7123
P-Value [Acc > NIR] : 0.656544
Kappa : 0.0823
Mcnemar's Test P-Value : 0.005578
Sensitivity : 0.14286
Specificity : 0.92308
Pos Pred Value : 0.42857
Neg Pred Value : 0.72727
Prevalence : 0.28767
Detection Rate : 0.04110
Detection Prevalence : 0.09589
Balanced Accuracy : 0.53297
'Positive' Class : 0
4.4 Árvores de Decisão
As árvores de decisão são um método gráfico e analítico que subdivide uma amostra inicial em subamostras, formando grupos onde a variável de resposta apresenta comportamento homogêneo internamente e heterogêneo entre eles. Este algoritmo de aprendizado de máquina supervisionado é aplicável tanto para classificação quanto para regressão, ou seja, pode prever tanto categorias discretas (como “sim” ou “não”) quanto valores numéricos (Singh and Allen 2016; Zbicki and Santos 2020):.
Funcionando de maneira semelhante a um fluxograma , as árvores de decisão têm nós de decisão interconectados hierarquicamente, incluindo um nó-raiz principal e nós-folha que representam os resultados finais. No machine learning, o nó-raiz corresponde a um atributo da base de dados, enquanto o nó-folha indica a classe ou valor a ser previsto (Singh and Allen 2016; Zbicki and Santos 2020).
Existem diversos algoritmos para a criação de árvores de decisão, sendo os mais comuns:
CHAID (Chi-square Automatic Interaction Detection): Este algoritmo é mais comumente usado para tarefas de classificação.Utiliza tabelas de contingência para identificar as melhores divisões.
CART (Classification and Regression Trees): Um dos algoritmos mais versáteis, o CART é utilizado tanto para regressão quanto para classificação. Sua abordagem binária para dividir os nós permite uma ampla gama de aplicações.
ID3 (Iteractive Dichotomizer 3): Geralmente aplicado em tarefas de classificação, mas existem versões para regressão, o ID3 seleciona atributos com base no Ganho de Informação, escolhendo aqueles que mais reduzem a incerteza no conjunto de dados.
C4.5: Uma evolução do ID3, o C4.5 inclui melhorias como o tratamento de dados contínuos e valores ausentes, mantendo a abordagem baseada em Ganho de Informação.
Árvores de decisão são particularmente úteis quando se deseja trabalhar com dados sem a necessidade de um tratamento extensivo. Elas lidam bem com valores atípicos e dados faltantes, reduzindo a necessidade de etapas de tratamento intensivo. Além disso, não é necessário converter dados categóricos para numéricos, pois este algoritmo lida eficientemente com informações nominais. Em situações que envolvem problemas tanto de classificação quanto de regressão, as árvores de decisão oferecem flexibilidade e eficácia, tornando-se uma escolha adequada para uma variedade de cenários analíticos.
4.4.1 Exemplo Prático
Implementação no R
Para ilustrar a utilização arvore de decisão, vamos utilizar o conjunto de dados aprovacao.xlsx, apresentado na seção anterior.
Pacotes Necessários
Prepararando os dados,
#Ler os dados e remover os NA
library(tidyverse)
library(readxl)
###Importar os dados
dados=read_excel("aprovacao.xlsx",1)
# Converter a variável Y para fator
dados$Y <- as.factor(dados$Y)
# Dividir o conjuntos de dados em treino e teste
set.seed(123)
training.samples <- dados$Y %>%
createDataPartition(p = 0.8, list = FALSE)
train.data <- dados[training.samples, ]
test.data <- dados[-training.samples, ]O seguinte código R constrói um modelo de árvore de decisão para prever se um indivíduo é positivo para diabetes com base em todas as variáveis preditoras disponíveis no conjunto de dados. Isso é realizado utilizando o operador ~ para incluir todas as variáveis preditoras:
Call:
rpart(formula = Y ~ ., data = train.data, method = "class")
n= 59
CP nsplit rel error xerror xstd
1 0.1470588 0 1.0000000 1.000000 0.2046323
2 0.1176471 2 0.7058824 1.294118 0.2184929
3 0.0100000 3 0.5882353 1.117647 0.2111212
Variable importance
X2 X1 X3 X5 X4
42 36 18 3 1
Node number 1: 59 observations, complexity param=0.1470588
predicted class=1 expected loss=0.2881356 P(node) =1
class counts: 17 42
probabilities: 0.288 0.712
left son=2 (34 obs) right son=3 (25 obs)
Primary splits:
X1 < 8.1 to the left, improve=3.7586840, (0 missing)
X2 < 2.5 to the right, improve=2.8023060, (0 missing)
X3 < 88.55 to the left, improve=1.3187740, (0 missing)
X5 < 5.55 to the left, improve=0.4445246, (0 missing)
X4 < 1.5 to the left, improve=0.3104132, (0 missing)
Surrogate splits:
X3 < 82.35 to the left, agree=0.644, adj=0.16, (0 split)
X5 < 2 to the right, agree=0.610, adj=0.08, (0 split)
X4 < 1.5 to the right, agree=0.593, adj=0.04, (0 split)
Node number 2: 34 observations, complexity param=0.1470588
predicted class=1 expected loss=0.4411765 P(node) =0.5762712
class counts: 15 19
probabilities: 0.441 0.559
left son=4 (23 obs) right son=5 (11 obs)
Primary splits:
X2 < 2.5 to the right, improve=3.99000200, (0 missing)
X5 < 4.55 to the left, improve=1.00081700, (0 missing)
X3 < 71.7 to the right, improve=0.92280860, (0 missing)
X1 < 5.8 to the right, improve=0.76470590, (0 missing)
X4 < 2.5 to the left, improve=0.02228164, (0 missing)
Node number 3: 25 observations
predicted class=1 expected loss=0.08 P(node) =0.4237288
class counts: 2 23
probabilities: 0.080 0.920
Node number 4: 23 observations, complexity param=0.1176471
predicted class=0 expected loss=0.3913043 P(node) =0.3898305
class counts: 14 9
probabilities: 0.609 0.391
left son=8 (15 obs) right son=9 (8 obs)
Primary splits:
X3 < 71.7 to the right, improve=1.339855000, (0 missing)
X5 < 4.55 to the left, improve=1.001976000, (0 missing)
X1 < 6.85 to the right, improve=0.797791600, (0 missing)
X2 < 7.5 to the left, improve=0.027950310, (0 missing)
X4 < 2.5 to the right, improve=0.006521739, (0 missing)
Surrogate splits:
X2 < 8.5 to the left, agree=0.783, adj=0.375, (0 split)
X1 < 6.5 to the right, agree=0.696, adj=0.125, (0 split)
Node number 5: 11 observations
predicted class=1 expected loss=0.09090909 P(node) =0.1864407
class counts: 1 10
probabilities: 0.091 0.909
Node number 8: 15 observations
predicted class=0 expected loss=0.2666667 P(node) =0.2542373
class counts: 11 4
probabilities: 0.733 0.267
Node number 9: 8 observations
predicted class=1 expected loss=0.375 P(node) =0.1355932
class counts: 3 5
probabilities: 0.375 0.625 Este código produz um resumo detalhado do modelo de árvore de decisão, que pode ser complexo de analisar. Para facilitar a visualização, podemos representar graficamente a árvore construída:
prp(tree_model)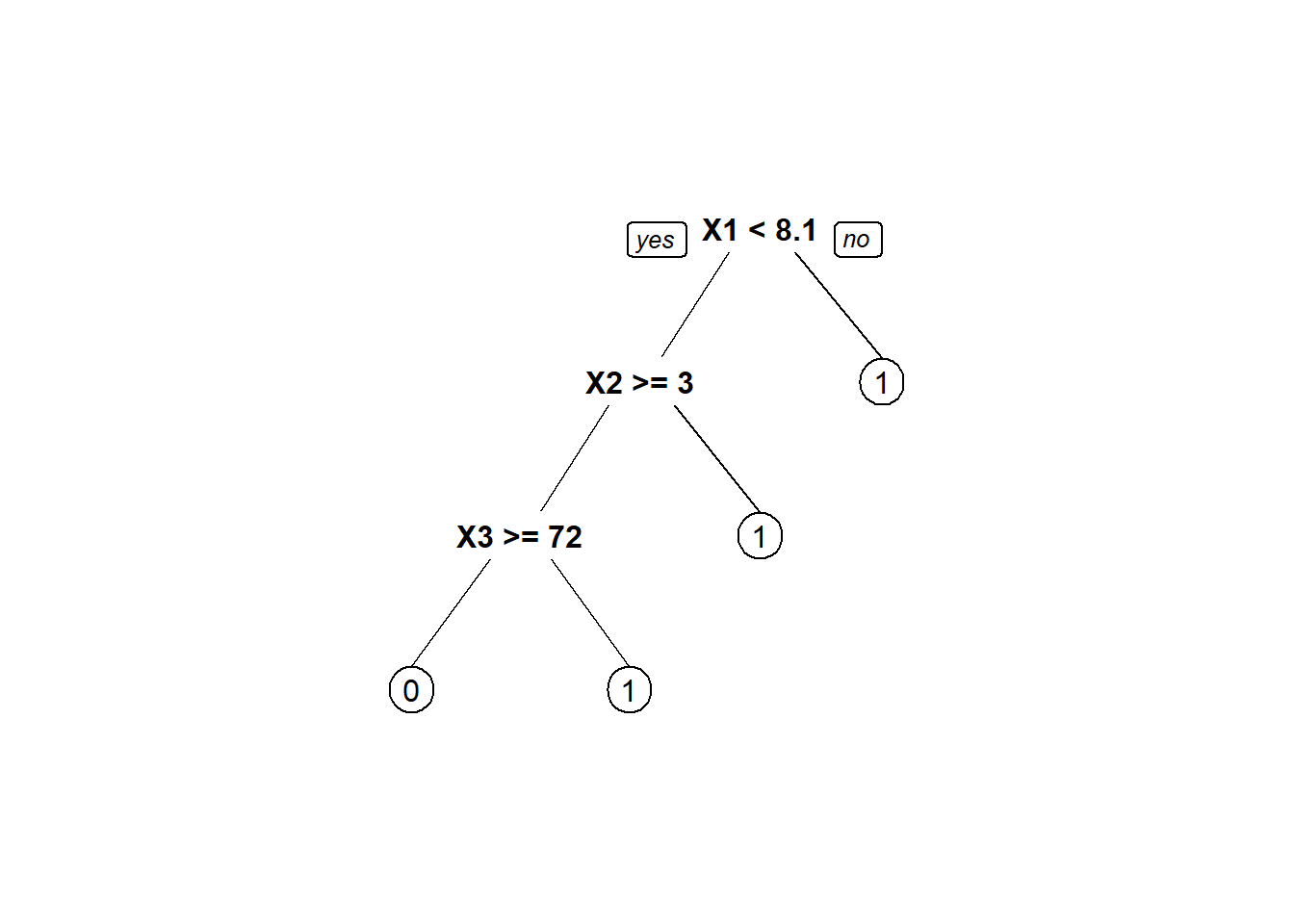
Este passo permite visualizar a estrutura da árvore de decisão de forma mais intuitiva e compreensível.
Por padrão, o rpart usa a impureza de Gini para selecionar divisões ao realizar classificação. (Se você não está familiarizado, leia este artigo.) Você pode usar o ganho de informação em vez disso, especificando-o no parâmetro parms.
tree_model1 <- rpart(Y ~.,data = train.data,method = "class",
parms = list(split = 'information')
)
prp(tree_model1)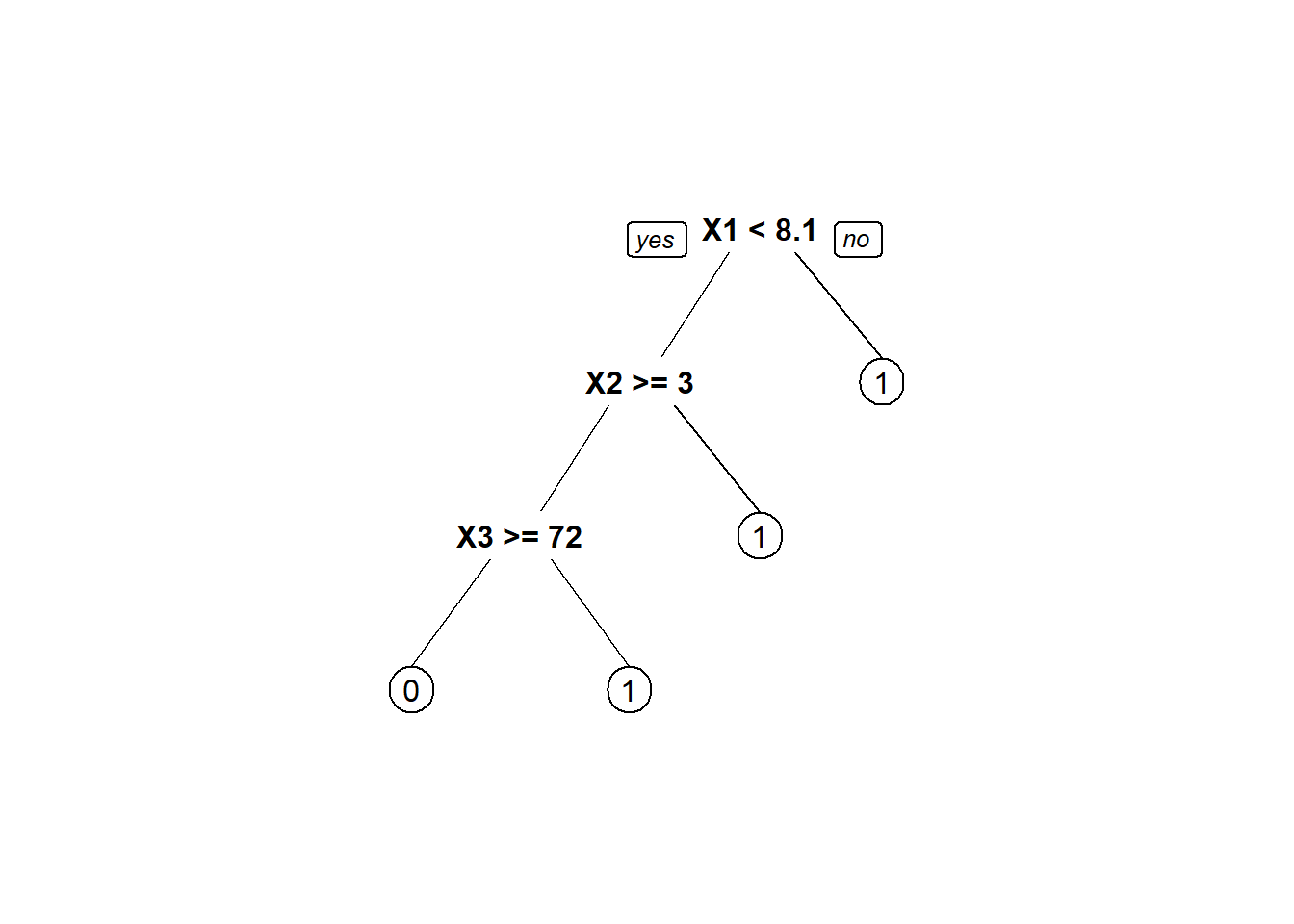
Podemos avaliar a capacidade preditiva do com os dados de treino e teste, utilizando os dados que ele já conhece através do seguinte processo no R:
# Predições de treinamento
class <- predict(tree_model1,type = 'class')
confusionMatrix(class, train.data$Y,positive="1")Confusion Matrix and Statistics
Reference
Prediction 0 1
0 11 4
1 6 38
Accuracy : 0.8305
95% CI : (0.7103, 0.9156)
No Information Rate : 0.7119
P-Value [Acc > NIR] : 0.02651
Kappa : 0.5718
Mcnemar's Test P-Value : 0.75183
Sensitivity : 0.9048
Specificity : 0.6471
Pos Pred Value : 0.8636
Neg Pred Value : 0.7333
Prevalence : 0.7119
Detection Rate : 0.6441
Detection Prevalence : 0.7458
Balanced Accuracy : 0.7759
'Positive' Class : 1
# Predições de teste
class1 <- predict(tree_model1,test.data,type = 'class')
confusionMatrix(class1, test.data$Y,positive="1")Confusion Matrix and Statistics
Reference
Prediction 0 1
0 0 2
1 4 8
Accuracy : 0.5714
95% CI : (0.2886, 0.8234)
No Information Rate : 0.7143
P-Value [Acc > NIR] : 0.9259
Kappa : -0.2353
Mcnemar's Test P-Value : 0.6831
Sensitivity : 0.8000
Specificity : 0.0000
Pos Pred Value : 0.6667
Neg Pred Value : 0.0000
Prevalence : 0.7143
Detection Rate : 0.5714
Detection Prevalence : 0.8571
Balanced Accuracy : 0.4000
'Positive' Class : 1
O resultado, com uma acurácia de 0,8305 para os dados de treinamento e 0.5714 para os dados de teste, indica que o modelo de regressão logística múltipla tem uma boa capacidade de generalização. Além disso, outras medidas de performance do modelo apresentam valores elevados.
4.5 Floresta Aleatória
Floresta Aleatória é um algoritmo de aprendizado supervisionado que cria uma “floresta” de forma aleatória. Essa floresta é na verdade um conjunto de árvores de decisão, geralmente treinadas com o método de bagging. A ideia por trás do bagging é que a combinação de vários modelos de aprendizado melhora o desempenho geral.
As Florestas Aleatórias funcionam ao criar numerosas árvores de decisão aleatoriamente, cada uma contribuindo para a decisão final. Uma grande vantagem desse algoritmo é sua aplicabilidade tanto em tarefas de classificação quanto de regressão, sendo muito relevante nos sistemas de aprendizado de máquina atuais. No contexto de classificação, as Florestas Aleatórias são consideradas um dos pilares do aprendizado de máquina. Um exemplo clássico de Floresta Aleatória pode incluir diversas árvores, cada uma contribuindo para a classificação ou previsão final.
Diferenças entre Árvore de Decisão e Florestas Aleatórias
Floresta Aleatória e Árvore de Decisão são métodos de aprendizado de máquina, mas com diferenças significativas. Enquanto a Árvore de Decisão utiliza regras e nodos baseados em cálculos como ganho de informação e índice de Gini, a Floresta Aleatória opera de maneira aleatória e é uma coleção de várias árvores. Uma Árvore de Decisão única pode sofrer de sobreajuste, especialmente se for muito profunda. Em contraste, as Florestas Aleatórias minimizam o sobreajuste ao construir várias árvores menores a partir de subconjuntos aleatórios de características, combinando-as posteriormente. Este processo pode tornar as Florestas Aleatórias mais lentas, dependendo do número de árvores construídas.
Algoritmo para Florestas Aleatórias
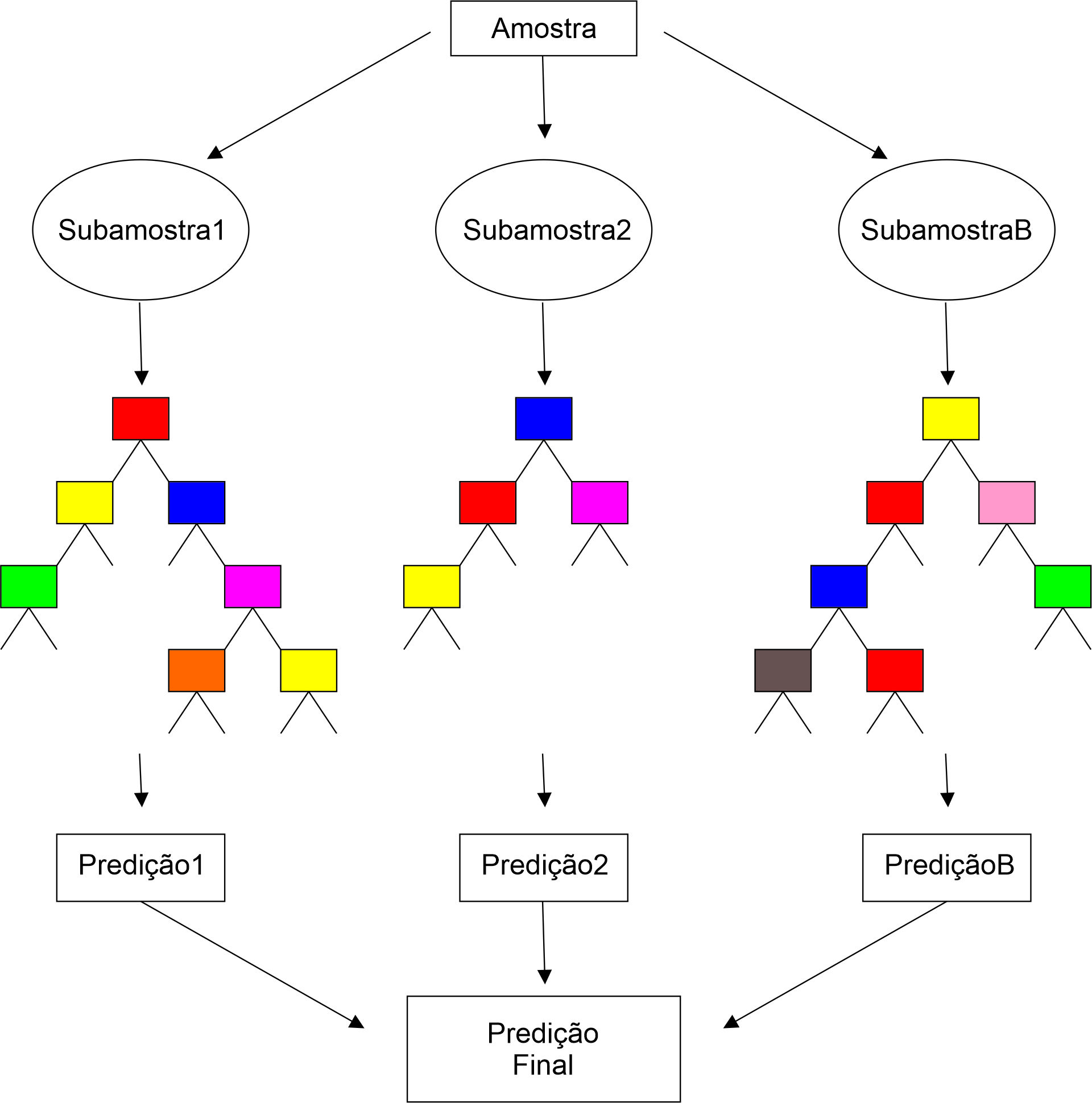
O algoritmo das Florestas Aleatórias (Random Forest) funciona da seguinte maneira:
Gerar \(B\) amostras bootstrap com reposição do conjunto de dados original.
-
Para cada amostra bootstrap, criar uma árvore de decisão:
Em cada nó, é sorteado \(M\) atributos dentre os quais a divisão será realizada.
A árvore é construída sem ser podada.
Cada árvore gera um resultado, e a classificação/regressão final é determinada pelo resultado mais frequente entre todas as árvores.
4.5.1 Exemplo Prático
Implementação no R
Para ilustrar a utilização arvore de decisão, vamos utilizar o conjunto de dados aprovacao.xlsx, apresentado na seção anterior.
Pacotes Necessários
Prepararando os dados,
#Ler os dados e remover os NA
library(tidyverse)
library(readxl)
###Importar os dados
dados=read_excel("aprovacao.xlsx",1)
# Converter a variável Y para fator
dados$Y <- as.factor(dados$Y)
# Dividir o conjuntos de dados em treino e teste
set.seed(123)
training.samples <- dados$Y %>%
createDataPartition(p = 0.8, list = FALSE)
train.data <- dados[training.samples, ]
test.data <- dados[-training.samples, ]O seguinte código R constrói um modelo de árvore de decisão para prever se um indivíduo é positivo para diabetes com base em todas as variáveis preditoras disponíveis no conjunto de dados. Isso é realizado utilizando o operador ~ para incluir todas as variáveis preditoras:
rf_model <- randomForest( Y ~., data = train.data)
print(rf_model)
Call:
randomForest(formula = Y ~ ., data = train.data)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 2
OOB estimate of error rate: 35.59%
Confusion matrix:
0 1 class.error
0 3 14 0.8235294
1 7 35 0.1666667Podemos avaliar a capacidade preditiva do com os dados de treino e teste, utilizando os dados que ele já conhece através do seguinte processo no R:
#Conjunto de treino
class <- predict(rf_model)
confusionMatrix(class, train.data$Y,positive='1')Confusion Matrix and Statistics
Reference
Prediction 0 1
0 3 7
1 14 35
Accuracy : 0.6441
95% CI : (0.5087, 0.7645)
No Information Rate : 0.7119
P-Value [Acc > NIR] : 0.9002
Kappa : 0.0112
Mcnemar's Test P-Value : 0.1904
Sensitivity : 0.8333
Specificity : 0.1765
Pos Pred Value : 0.7143
Neg Pred Value : 0.3000
Prevalence : 0.7119
Detection Rate : 0.5932
Detection Prevalence : 0.8305
Balanced Accuracy : 0.5049
'Positive' Class : 1
#Conjunto de teste
class1 <- predict(rf_model,test.data)
confusionMatrix(class1,test.data$Y,positive='1')Confusion Matrix and Statistics
Reference
Prediction 0 1
0 0 1
1 4 9
Accuracy : 0.6429
95% CI : (0.3514, 0.8724)
No Information Rate : 0.7143
P-Value [Acc > NIR] : 0.8152
Kappa : -0.129
Mcnemar's Test P-Value : 0.3711
Sensitivity : 0.9000
Specificity : 0.0000
Pos Pred Value : 0.6923
Neg Pred Value : 0.0000
Prevalence : 0.7143
Detection Rate : 0.6429
Detection Prevalence : 0.9286
Balanced Accuracy : 0.4500
'Positive' Class : 1
O resultado, com uma acurácia de 0,6441 para os dados de treinamento e 0,6429 para os dados de teste, indica que o modelo de regressão logística múltipla tem uma boa capacidade de generalização. Além disso, outras medidas de performance do modelo apresentam valores elevados.
4.6 Introdução ao CARET
O pacote caret (Kuhn and Max 2008) (Classification And REgression Training) no R é uma ferramenta valiosa para simplificar o treinamento de modelos em problemas complexos de regressão e classificação. Este pacote integra diversos outros pacotes do R, mas é projetado para carregá-los conforme a necessidade, evitando o carregamento de todos eles na inicialização. Isso reduz significativamente o tempo de inicialização do pacote e melhora a eficiência. O caret assume que os pacotes necessários estão instalados e, caso algum pacote de modelagem esteja faltando, ele notifica o usuário para instalá-lo. Sua popularidade se deve à sua capacidade de simplificar as etapas de treinamento e teste de modelos preditivos. Para exemplos detalhados de como utilizar o caret, pode-se visitar a página oficial: Caret Package.
O pacote caret no R oferece uma ampla gama de ferramentas para a preparação de dados, essencial para o sucesso dos modelos de machine learning. Ele facilita a normalização e padronização de dados, o que é crucial para métodos que são sensíveis à escala das variáveis. Além disso, o caret pode tratar dados faltantes, realizar a binarização de variáveis categóricas e a seleção de variáveis, ajudando a melhorar a eficiência e a eficácia dos modelos. Esses recursos tornam o caret uma escolha excelente para o preprocessamento de dados antes da aplicação de técnicas de aprendizado de máquina.
O caret proporciona uma interface unificada para uma ampla gama de modelos de machine learning, permitindo aos usuários aplicar diversos métodos e técnicas com uma sintaxe consistente. Isso inclui desde modelos lineares até técnicas avançadas de ensemble.
4.6.1 Treinamento de modelos
Para ilustrar a utilização arvore de decisão, vamos utilizar o conjunto de dados aprovacao.xlsx, apresentado na seção anterior. e vamos obter um modelo de arvore de decisão.
Uma das funções centrais do pacote caret é a train(), que é essencial para a construção de modelos de machine learning. Esta função automatiza o processo de treinamento, incorporando técnicas como validação cruzada e otimização de parâmetros. Ao usar a train(), o usuário pode aplicar diversos algoritmos aos dados, resultando em modelos bem treinados e prontos para serem testados e usados em previsões. A função train também facilita a comparação do desempenho de diferentes algoritmos, tornando-a uma ferramenta valiosa para a seleção de modelos adequados.
Pacotes Necessários
Prepararando os dados,
#Ler os dados e remover os NA
library(tidyverse)
library(readxl)
###Importar os dados
dados=read_excel("aprovacao.xlsx",1)
# Converter a variável Y para fator
dados$Y <- as.factor(dados$Y)
# Dividir o conjuntos de dados em treino e teste
set.seed(123)
training.samples <- dados$Y %>%
createDataPartition(p = 0.8, list = FALSE)
train.data <- dados[training.samples, ]
test.data <- dados[-training.samples, ]Treinar o modelo
tree_model <- train(Y ~., data = train.data, method = "rpart")
#Resultados do modelo
tree_model$results cp Accuracy Kappa AccuracySD KappaSD
1 0.0000000 0.7003162 0.2441206 0.07770663 0.2042033
2 0.1176471 0.6915064 0.2255456 0.08066970 0.2086482
3 0.1470588 0.6932455 0.2348267 0.07926648 0.2058785tree_model$bestTune cp
1 0tree_model$metric[1] "Accuracy"#Plotar a arvore obtida
m=tree_model$finalModel
prp(m, box.palette = "Reds", tweak = 1.2)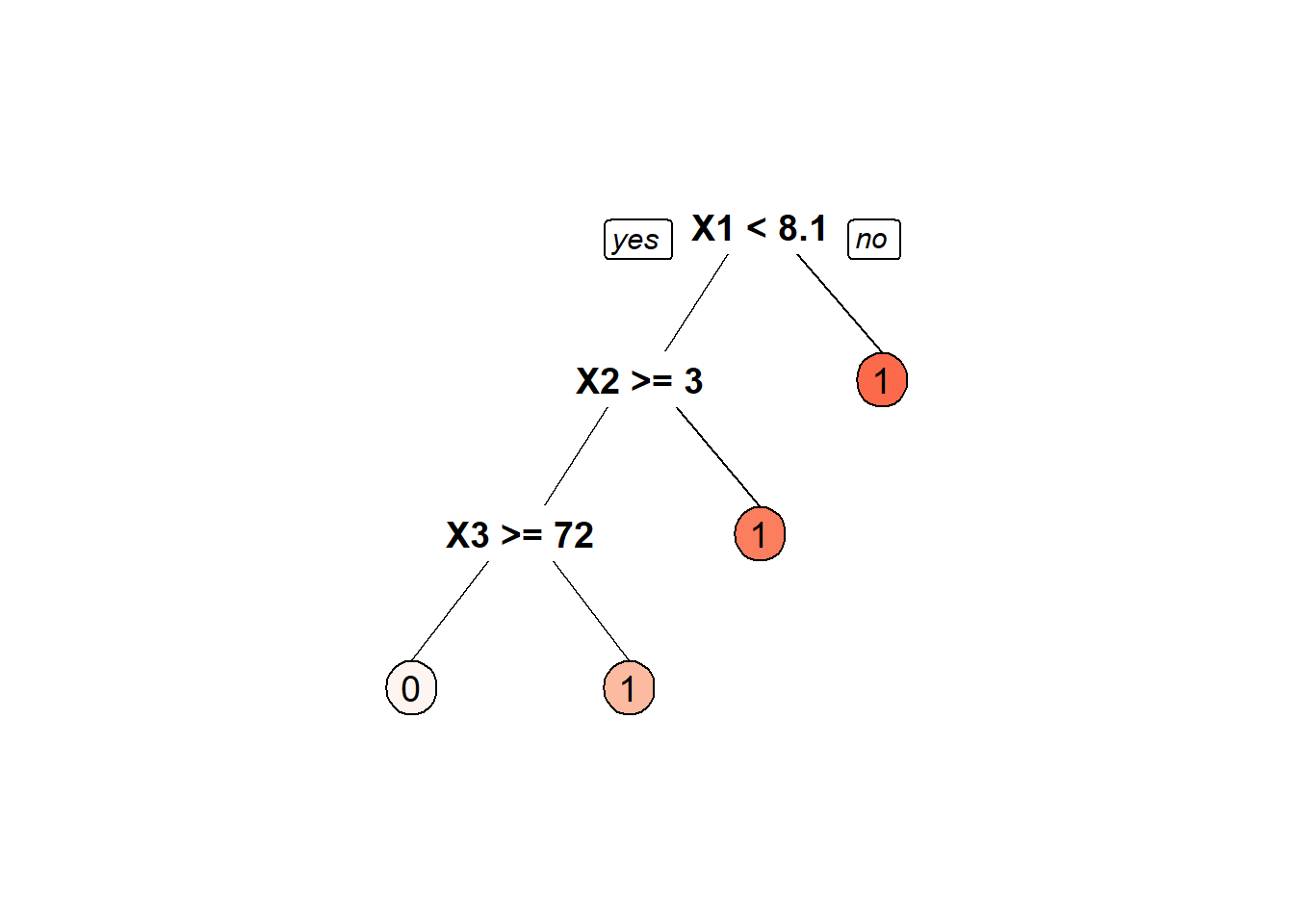
O tuneGrid é uma funcionalidade importante do pacote caret no R, utilizada para otimizar os hiperparâmetros de modelos de machine learning. Com o tuneGrid, os usuários podem especificar uma grade de hiperparâmetros que o caret irá explorar durante o treinamento do modelo. Isso permite a identificação da combinação de parâmetros que resulta no melhor desempenho do modelo, otimizando assim a precisão das previsões. Esta ferramenta é essencial para refinar modelos e garantir que eles estejam operando em sua capacidade máxima.
No caso de árvores de decisão, um hiperparâmetro importante é o parâmetro de complexidade (cp), que determina a poda da árvore. Este parâmetro ajuda a controlar o tamanho da árvore e a evitar overfitting. Ao utilizar o tuneGrid no caret para uma árvore de decisão, você pode especificar diferentes valores de cp para encontrar o que proporciona o melhor equilíbrio entre a complexidade da árvore e a capacidade de generalização do modelo.
hyper=expand.grid(
cp = seq(0.005, 1.0, 0.005) #parametros de complexidade de 0.005 até 1.0
)
tree_model <- train(Y ~., data = train.data, method = "rpart",tuneGrid=hyper)
##Visuzalizar as acuráciass em função do parametro de complexidade
plot(tree_model)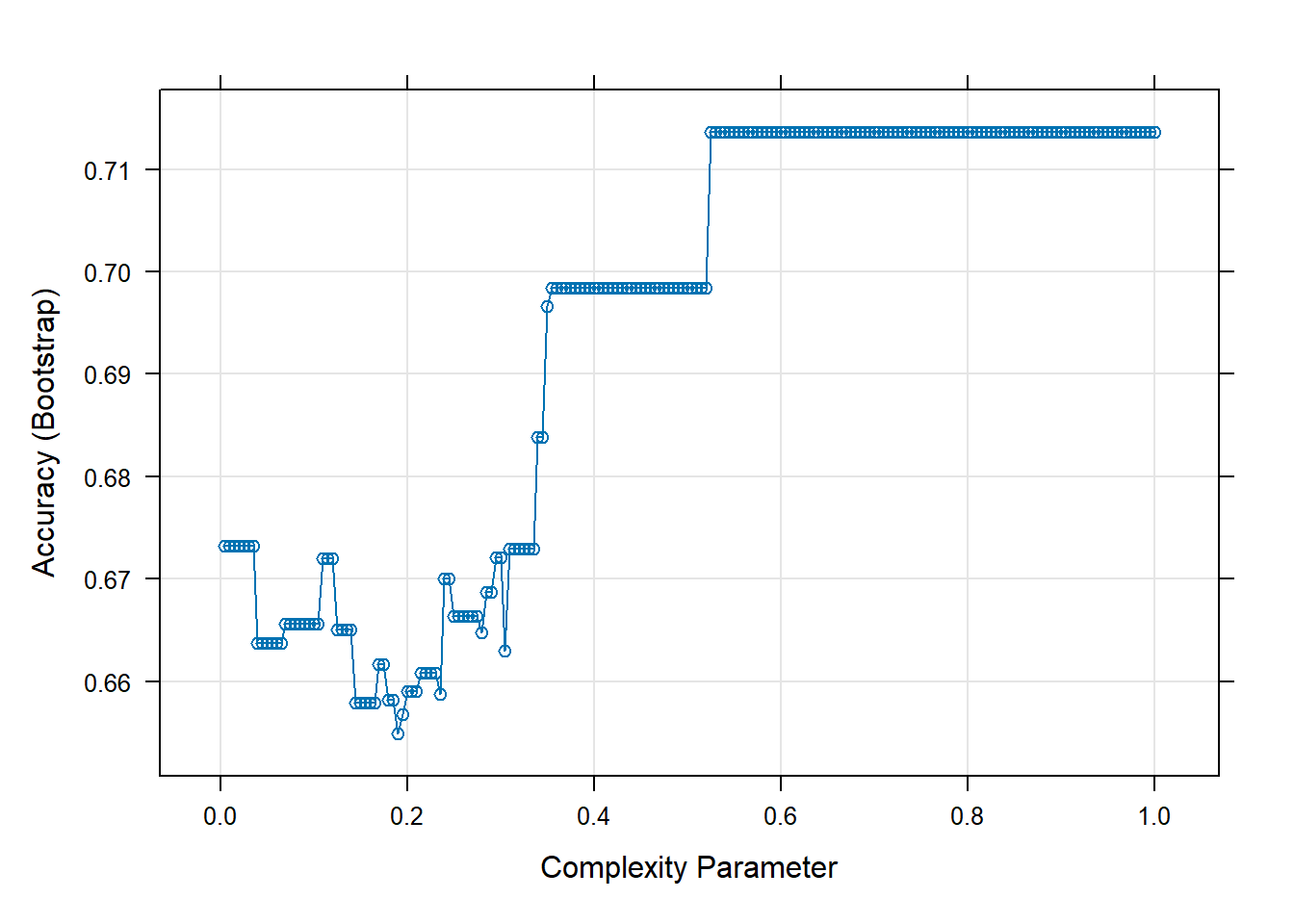
#Resultados do modelo
tree_model$bestTune cp
200 1tree_model$metric[1] "Accuracy"#Plotar a arvore obtida
m=tree_model$finalModel
prp(m, box.palette = "Reds", tweak = 1.2)
Para a validação de modelos no caret, métodos como a validação cruzada k-fold e bootstrap são disponibilizados através do argumento trControl na função train. Essas técnicas são essenciais para evitar o overfitting e avaliar a capacidade de generalização do modelo. A validação cruzada k-fold divide o conjunto de dados em k partes, treinando o modelo em k-1 partes e testando-o na parte restante. O processo é repetido para cada parte. Já o método bootstrap utiliza amostragem com reposição para criar conjuntos de treino e teste, fornecendo uma avaliação robusta do modelo.
#Definir o hiperametros
hyper=expand.grid(
cp = seq(0.005, 1.0, 0.005) # complexidade de 0.005 até 1.0
)
#VAlidação K-fold
ctrl=trainControl(method="cv",number=10)
tree_model <- train(Y ~., data = train.data, method = "rpart",tuneGrid=hyper,trControl = ctrl,)
##Visuzalizar as acuráciass em função do parametro de complexidade
plot(tree_model)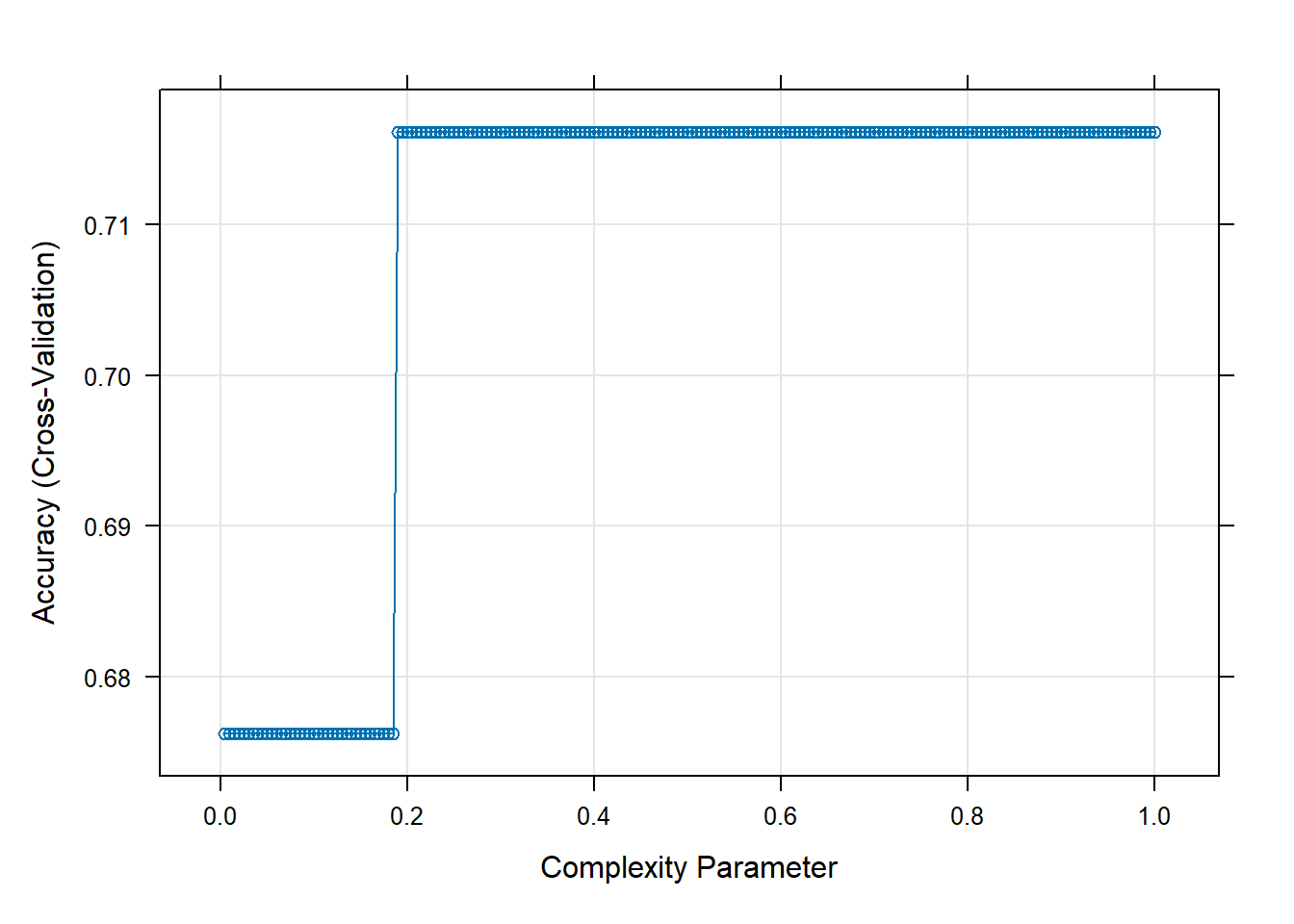
#Resultados do modelo
tree_model$bestTune cp
200 1tree_model$metric[1] "Accuracy"#Plotar a arvore obtida
m=tree_model$finalModel
prp(m, box.palette = "Reds", tweak = 1.2)
No contexto de dados desbalanceados, o caret oferece técnicas de amostragem na configuração trControl da função train. Essas técnicas incluem Sobreamostragem (para aumentar a presença da classe minoritária), Subamostragem (para diminuir a presença da classe majoritária), SMOTE (Synthetic Minority Over-sampling Technique) e ROSE (Random Over-Sampling Examples). Estas são fundamentais para assegurar que o modelo de machine learning não fique enviesado em favor da classe mais representada no conjunto de dados. A utilização adequada destas técnicas ajuda a melhorar a performance do modelo em dados desbalanceados.
#Definir o hiperametros
hyper=expand.grid(
cp = seq(0.005, 1.0, 0.005) # complexidade de 0.005 até 1.0
)
#VAlidação K-fold e sobreamostragem (Oversampling)
ctrl=trainControl(method="cv",number=10,
sampling = "up")
tree_model <- train(Y ~., data = train.data, method = "rpart",tuneGrid=hyper,trControl = ctrl,)
##Visuzalizar as acuráciass em função do parametro de complexidade
plot(tree_model)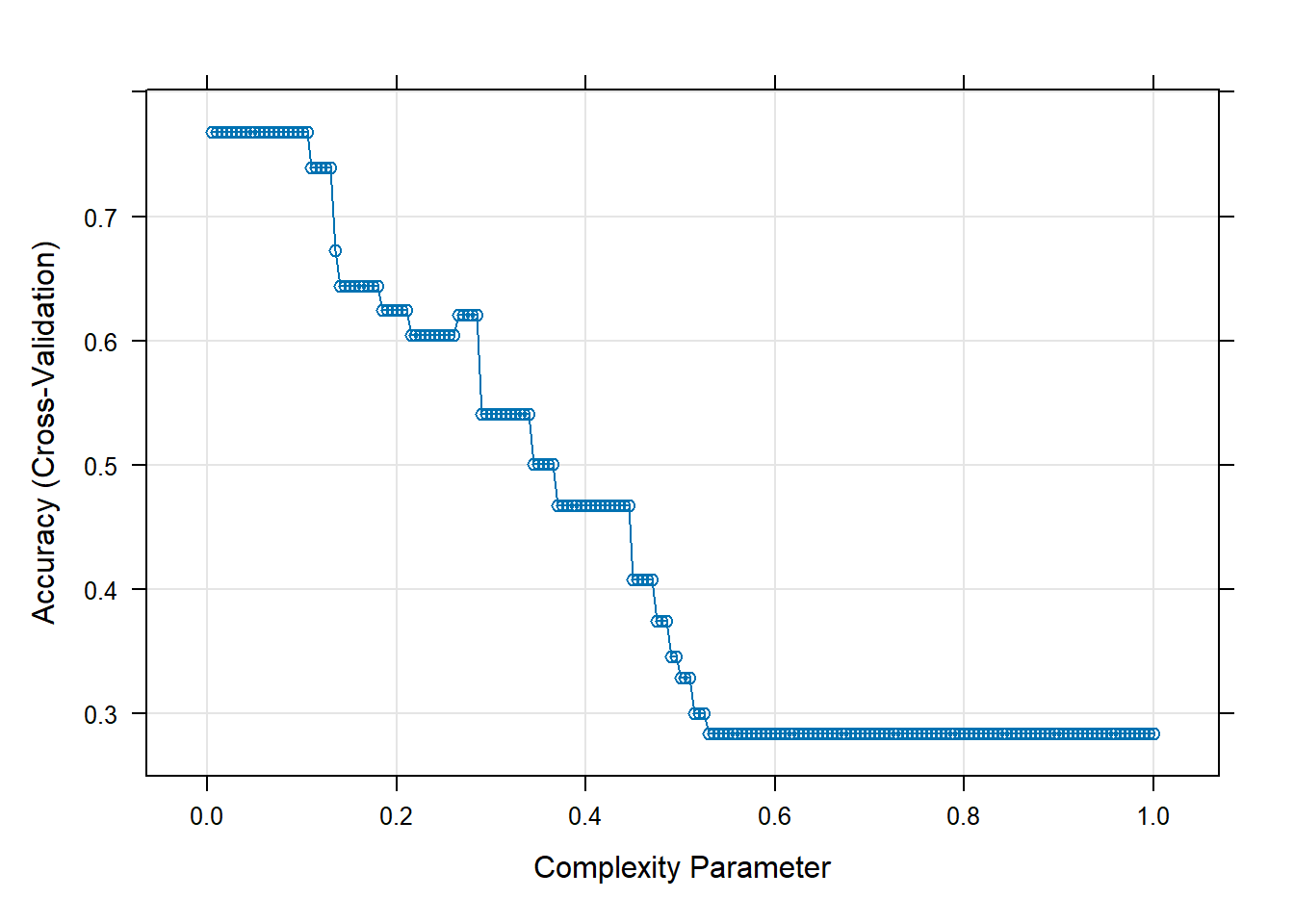
#Resultados do modelo
tree_model$bestTune cp
21 0.105tree_model$metric[1] "Accuracy"#Plotar a arvore obtida
m=tree_model$finalModel
prp(m, box.palette = "Reds", tweak = 1.2)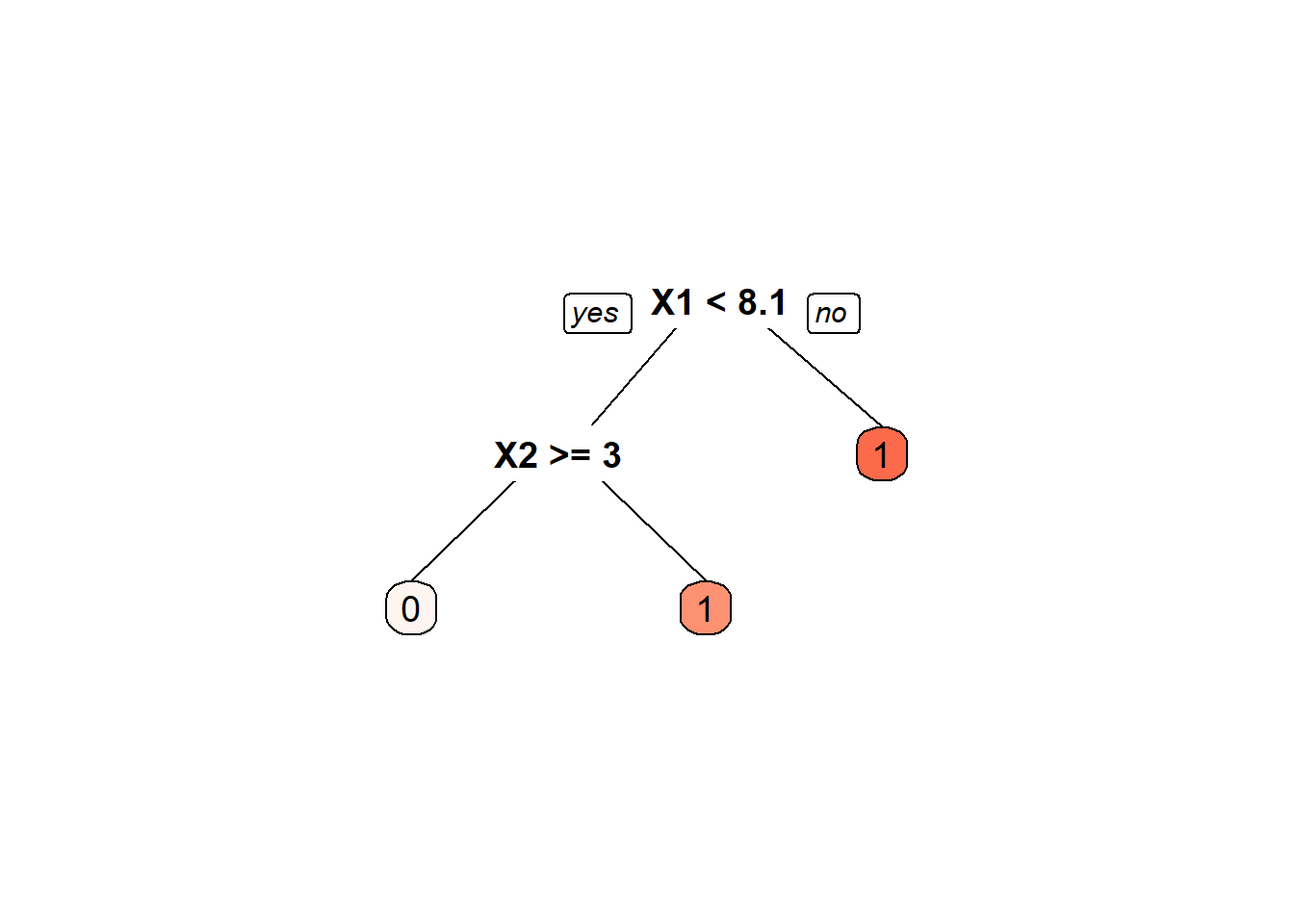
4.7 Tendências e Avanços na Machine Learning no R
Redes Neurais: No R, a implementação de redes neurais é facilitada por pacotes como
nnet(Venables and Ripley 2002) eneuralnet(Fritsch, Guenther, and Wright 2019), que permitem a criação de modelos de rede neural para uma variedade de tarefas de classificação e regressão. Essas redes são fundamentais para entender conceitos básicos de IA antes de avançar para técnicas mais complexas.Máquinas de Vetores de Suporte (SVM): R oferece suporte a SVMs por meio de pacotes como
e1071(Meyer et al. 2023), permitindo a construção de modelos eficazes para classificação e regressão, especialmente úteis em conjuntos de dados de alta dimensão.Deep Learning: O R tem visto um crescimento significativo na integração com tecnologias de Deep Learning. Pacotes como
keras(Allaire and Chollet 2023) etensorflow(Allaire and Tang 2023) permitem aos usuários do R acessar e implementar redes neurais profundas de forma eficiente. Esses pacotes trazem a potência do Deep Learning para a comunidade R, permitindo aplicações em visão computacional, reconhecimento de fala e outras áreas avançadas de IA.Aprendizado por Reforço: Uma área em expansão no R é o Aprendizado por Reforço, onde o objetivo é desenvolver modelos que aprendem a tomar decisões otimizadas. Pacotes como
ReinforcementLearning (Proellochs and Feuerriegel 2020) emarkovchain(Spedicato 2017) estão facilitando a implementação desses complexos algoritmos de aprendizado.AutoML: A automatização no processo de Machine Learning é uma tendência crescente. No R, ferramentas como o
automl(Boulangé 2020) estão simplificando o processo de seleção e otimização de modelos, tornando a Machine Learning acessível até mesmo para aqueles com menos experiência técnica.Interpretabilidade e Ética em IA: Com o aumento da complexidade dos modelos, a necessidade de interpretabilidade e considerações éticas se tornou mais premente. Pacotes como
lime(Hvitfeldt, Pedersen, and Benesty 2022)eDALEX(Biecek 2018) estão na vanguarda, fornecendo ferramentas para explicar e interpretar modelos complexos, e abordar questões éticas.Integração com Big Data: A capacidade de trabalhar com grandes volumes de dados é crucial. Pacotes como
sparklyr(Luraschi et al. 2023)oferecem integração com Apache Spark, permitindo o processamento de grandes conjuntos de dados dentro do ambiente R.-
Modelagem Bayesian: Métodos Bayesianos estão ganhando tração no R para uma ampla variedade de aplicações. Pacotes como
brms(Bürkner 2017) erstan(2023) oferecem frameworks avançados para modelagem estatística Bayesiana.Essas tendências demonstram como o R está evoluindo e se adaptando às necessidades de uma paisagem de dados em rápida mudança, mantendo-se como uma ferramenta valiosa e relevante no campo do Machine Learning.